Skip to content

\(C01-02\) Intervalles

Intervalles de nombres réels

Définition

Soient \(a\) et \(b\) deux nombres réels tels que \(a \leqslant b\).

  • On appelle intervalle fermé \([a;b]\) l’ensemble des nombres réels \(x\) tels que \(a\leqslant x\leqslant b\).

    img1

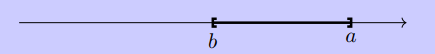
  • On appelle intervalle ouvert \(]a;b[\) l’ensemble des nombres réels \(x\) tels que \(a<x<b\).

    img2

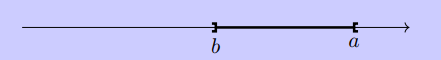
  • On définit de même les intervalles \([a;b[\) et \(]a;b]\).
  • On note \([a;+\infty[\) l’ensemble des nombres réels \(x\) tels que \(x\geqslant a\).

    img3

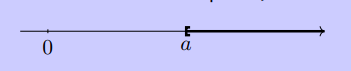
  • On note \(]a;+\infty[\) l’ensemble des nombres réels \(x\) tels que \(x>a\).

    img4

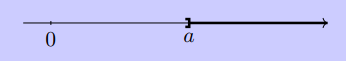
  • On définit de même \(]- \infty;a]\) et \(]-\infty;a[\).

Remarques

  • Le symbole \(+\infty\) se lit " Plus l'infini ".
  • Le symbole \(-\infty\) se lit " Moins l'infini ".
Représenter des intervalles

Ecrire les inégalités suivantes sous la forme d'un intervalle, puis représenter cet intervalle sur la droite des réels :

  1. \(x\leqslant 5\)
  2. \(x>-3\)
  3. \(2<x<5\)
  4. \(-4\leqslant x \leqslant -3\)
  5. \(-3\leqslant x < 8\)
  6. \(-2< x \leqslant 0\)
  1. \(]-\infty ; 5]\)
  2. \(]-3 ; +\infty[\)
  3. \(]2;5[\)
  4. \([-4;-3]\)
  5. \([-3;8[\)
  6. \(]-2;0]\)
Appartient ou pas ?

Compléter avec un symbole \(\in\) ou \(\notin\) :

  • \(-2 \dots [-2; 1[\)
  • \(-3 \dots [-5; -1[\)
  • \(-\dfrac{26}{5} \dots ]-5; -4[\)
  • \(4 \dots [-3; 4[\)
  • \(2\pi \dots [7;8]\)
  • \(0 \dots \mathbb{R}\)
  • \(0 \dots \mathbb{R}^*\)
  • \(-2 \in [-2; 1[\)
  • \(-3 \in [-5; -1[\)
  • \(-\dfrac{26}{5} \notin ]-5; -4[\)
  • \(4 \notin [-3; 4[\)
  • \(2\pi \notin [7;8]\)
  • \(0 \in \mathbb{R}\)
  • \(0 \notin \mathbb{R}^*\)
Travailler les représentations

Recopier et compléter :

tab

A venir....

Unions et intersections d'intervalles

Définition

Soient \(I\) et \(J\) deux intervalles.

  • L’intersection de \(I\) et \(J\) est l’ensemble des réels qui appartiennent à la fois à \(I\) \textbf{ET} à \(J\). On note cet ensemble \(I \cap J\).
  • La réunion de \(I\) et \(J\) est l’ensemble des réels qui appartiennent à \(I\) \textbf{OU} à \(J\). On note cet ensemble \(I \cup J\).

Remarques

  • La notation \(\cap\) se lit \og inter \fg. D'où \(I \cap J\) se lit \og \(I\) inter \(J\) \fg.
  • La notation \(\cup\) se lit \og union \fg. D'où \(I \cup J\) se lit \og \(I\) union \(J\) \fg.
  • Parfois, il n'y a aucun élément qui appartiennent à la fois à \(I\) et \(J\). L'intersection est donc \textbf{vide}, et on note \(\emptyset\) l'ensemble vide. Dans ce cas \(I \cap J = \emptyset\).

Exemple

On considère les intervalles \(I=[3;7]\) et \(J=]2; 5[\).

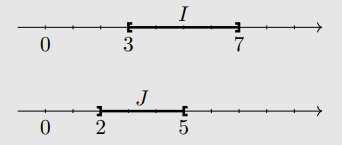
2inter

  • L'ensemble \(I\cap J\) est \([3;5[\).

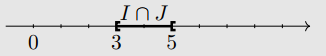
    intersect

  • L'ensemble \(I\cup J\) est \(]2;7]\).

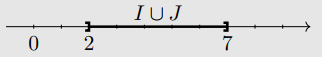
    intersect

Utiliser les notations \(\cap\) et \(\cup\)

R\'eduire sous la forme d'un seul intervalle si possible et représenter sur la droite des réels :

  • \(]-3;7] \cap ]-2;8[\)
  • \(]-4;3] \cap [-2;3,5[\)
  • \([-7;4[ \cup ]-3;5]\)
  • \(]-3;5] \cup [-1;2]\)
  • \([-6;6]\cup[-2;2]\)
  • \(]-\infty;2[ \cap ]1;+\infty[\)
  • \(]-\infty;-1] \cup ]2;6]\)
  • \([-5;3] \cap [6;8]\)
  • \(]-3;7] \cap ]-2;8[ = ]-2;7]\)
  • \(]-4;3] \cap [-2;3,5[ = [-2;3]\)
  • \([-7;4[ \cup ]-3;5] = [-7;5]\)
  • \(]-3;5] \cup [-1;2] = ]-3;5]\)
  • \([-6;6]\cup[-2;2] = [-6;6]\)
  • \(]-\infty;2[ \cap ]1;+\infty[ = ]1;2[\)
  • \(]-\infty;-1] \cup ]2;6] = ]-\infty;-1] \cup ]2;6]\)
  • \([-5;3] \cap [6;8] = \emptyset\)

Ensemble vide

L'ensemble vide est noté \(\emptyset\).

Travailler les inéquations et les intervalles

Compléter en s'aidant de la méthode donnée dans l'exemple ci-dessous.

Exemple

On a les équivalences :

\(x \in [1;2]\) \(\Longleftrightarrow\) \(1 \leqslant x \leqslant 2\) par définition
\(\Longleftrightarrow\) \(3 \leqslant 3x \leqslant 6\) en multipliant chaque membre de l'inégalité par \(3\)
\(\Longleftrightarrow\) \(3x \in [3;6]\) par définition

d'où \(x \in [1;2]\) si et seulement si \(3x \in [3;6]\)

  1. \(x \in [7;20]\) si et seulement si \(7x \in \dots\)
  2. \(x \in ]-1;3]\) si et seulement si \(x+4 \in \dots\)
  3. \(x \in [2;6]\) si et seuelemnt si \(8-x \in \dots\)
  4. \(x \in \dots\) si et seulement si \(x+6 \in ]3 ; +\infty[\)
  5. \(x \in \dots\) si et seulement si \(-2x \in [4 ; +\infty[\)
  6. \(x \in \dots\) si et seulement si \(4x+3 \in [-6;5]\)
  1. \(x \in [7;20]\) si et seulement si \(7x \in [49;140]\)
  2. \(x \in ]-1;3]\) si et seulement si \(x+4 \in ]3;7]\)
  3. \(x \in [2;6]\) si et seuelemnt si \(8-x \in [2;6]\)
  4. \(x \in ]-3 ; +\infty[\) si et seulement si \(x+6 \in ]3 ; +\infty[\)
  5. \(x \in ]-\infty ; -2]\) si et seulement si \(-2x \in [4 ; +\infty[\)
  6. \(x \in [-\dfrac{9}{4};2]\) si et seulement si \(4x+3 \in [-6;5]\)
Représenter sous la forme d'intervalles
  • \(y>-3\) et \(y<4\)
  • \(y>-3\) ou \(y<4\)
  • \(y \leqslant \dfrac{1}{3}\) et \(y \leqslant \dfrac{1}{2}\)
  • \(y \leqslant \dfrac{1}{3}\) ou \(y \leqslant \dfrac{1}{2}\)

A venir

Résolutions d'équations du premier degré

  1. Résoudre dans \(\mathbb{R}\) chacune des équations suivantes :

  2. \(3x -6 =0\)

  3. \(3x -4 = 0\)
  4. \(-3x +64 = 19\)
  5. \(-2(x+5)=-8\)
  6. \(3x -\pi=0\)

  7. \(\dfrac{x-8}{3}=-4\)

  8. Lesquelles de ces 4 équations sont résolubles dans \(\mathbb{Z}\) ? Dans \(\mathbb{Q}\) ?

A venir

Résolutions d'inéquations du premier degré

Résoudre les inéquations suivantes et présenter le résultat sous la forme d'un intervalle :

  • \(3x -6 >0\)
  • \(3x -4 \leqslant 0\)
  • \(-3x +64 < 19\)