C01-01 : Ensembles de Nombres

La version pdf de ce cours est téléchargeable ici. (version 2021-2022)

Activité : Classer des nombres

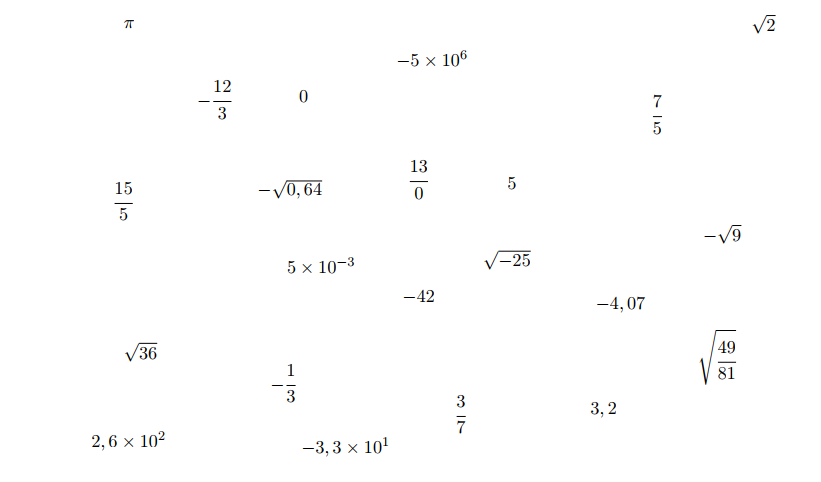
liste de nombres

Dans la liste ci-dessus, deux écritures sont interdites. Lesquelles et pourquoi ?
Classer les nombres restants en cinq groupes, en justifiant vos choix.

Différence entres propriétés et écritures

Un nombre peut être écrit de différentes manières, plus ou moins compliquées. Par exemple :

\[ 2 = \cfrac{6}{3} = 20 \times 10^{-1} = \sqrt{4}= - \left(-2\right) = 2,0000 \]

Pour autant, ce qui nous intéresse en mathématiques c'est d'étudier les propriétés de ce nombre, qui elles sont indépendantes de l'écriture de ce nombre.

Nombres entiers naturels et relatifs

Définitions

L'ensemble des entiers naturels, noté $\mathbb{N}$, est l'ensemble des nombres permettant de dénombrer une collection d'objets, de personnes, etc, c'est-à-dire la suite naturelle $0~;~1~;~2~;~3~;~...$
L'ensemble des entiers relatifs, noté $\mathbb{Z}$, est l'ensemble des entiers naturels et leurs opposés, c'est-à-dire la suite $...~;~-3~;~-2~;~-1~;~0~;~1~;~2~;~3~;~...$

Info

L'ensemble $\mathbb{N}$ possède un plus petit élément, c'est $0$.
Les nombres entiers naturels sont tous positifs ou nuls.
Tous les entiers naturels sont aussi des entiers relatifs.

Vocabulaire et notations

Appartenance : On dit que $5$ appartient à $\mathbb{N}$, et on note $5 \in \mathbb{N}$. De même $-2$ n'appartient pas à $\mathbb{N}$, et on note $-12 \notin \mathbb{N}$.
Inclusion : Tous les éléments de $\mathbb{N}$ sont aussi des éléments de $\mathbb{Z}$. On dit alors que $\mathbb{N}$ est un sous-ensemble de $\mathbb{Z}$ et on note alors $\mathbb{N} \subset \mathbb{Z}$ (qui se lit $\mathbb{N}$ est inclus dans $\mathbb{Z}$).

Application : choix du bon symbole

ExerciceSolution

Compléter avec $\in$ ou $\notin$ :

$7 \dots \mathbb{N}$

$-3 \dots \mathbb{N}$

$-5 \dots \mathbb{Z}$

$7 \dots \mathbb{Z}$

$\dfrac{1}{3} \dots \mathbb{N}$

$\sqrt{9} \dots \mathbb{N}$

$-\sqrt{25} \dots \mathbb{N}$

$-\sqrt{2} \dots \mathbb{Z}$

$5 \times 10^{3} \dots \mathbb{N}$

$5 \times 10 ^{-3} \dots \mathbb{Z}$

$-4,2 \dots \mathbb{Z}$

$3 \times (1 - \dfrac{1}{3}) \dots \mathbb{N}$

Compléter avec $\in$ ou $\notin$ :

$7 \in \mathbb{N}$

$-3 \notin \mathbb{N}$

$-5 \in \mathbb{Z}$

$7 \in \mathbb{Z}$

$\dfrac{1}{3} \notin \mathbb{N}$

$\sqrt{9} \in \mathbb{N}$ car $\sqrt{9} = 3$

$-\sqrt{25} \notin \mathbb{N}$ car $-\sqrt{25} = -5$

$-\sqrt{2} \notin \mathbb{Z}$ car $-\sqrt{2} \simeq -1,414...$

$5 \times 10^{3} \in \mathbb{N}$ car $5 \times 10^3 = 5 \times 1000 = 5000$

$5 \times 10 ^{-3} \notin \mathbb{Z}$ car $5 \times 10 ^{-3} = 5 \times 0,001 = 0,005$

$-4,2 \notin \mathbb{Z}$

$3 \times (1 - \dfrac{1}{3}) \in \mathbb{N}$ car $3 \times (1 - \dfrac{1}{3}) = 3 - 1 = 2$ (en développant) ou $3 \times (1 - \dfrac{1}{3}) = 3 \times \dfrac{2}{3} = 2$ (en calculant entre parenthèses).

Nombres décimaux

définition : Nombres décimaux

Un nombre décimal est un nombre pouvant s'écrire sous la forme d'une fraction décimale, c'est à dire sous la forme $$ \dfrac{a}{10^n} $$ avec $a\in \mathbb{Z}$ et $n\in \mathbb{N}$.

L'ensemble des décimaux est noté $\mathbb{D}$.

Application : Nombres décimaux et puissances de 10

ExerciceSolution

Pour chacun des nombres suivants, déterminer si possible une écriture de la forme $\dfrac{k}{10^n}$.

$4,37$

$0,002$

$-12$

$\dfrac{1}{3}$

$\dfrac{2}{5}$

$\sqrt{0,16}$

$10^3$

$10^{-5}$

$-10^5$

$\dfrac{3.10^5}{10^7}$

$\dfrac{10^7}{3.10^5}$

Pour chacun des nombres suivants, déterminer si possible une écriture de la forme $\dfrac{k}{10^n}$.

$4,37 = \dfrac{437}{100} = \dfrac{437}{10^{2}}$

$0,002 = \dfrac{2}{1~000} = \dfrac{2}{10^{3}}$

$-12 = \dfrac{-12}{1} = \dfrac{-12}{10^{0}}$ ( car $a^0 =1$ pour tout nombre $a \neq 0$).

$\dfrac{1}{3} \notin \mathbb{D}$ car $\dfrac{1}{3} \simeq 0,333...$ (La démonstration réelle sera donnée plus tard dans l'année)

$\dfrac{2}{5} = \dfrac{4}{10} = \dfrac{4}{10^1}$

$\sqrt{0,16} = 0,4 = \dfrac{4}{10} = \dfrac{4}{10^1}$

$10^3 = \dfrac{1~000}{1} = \dfrac{1~000}{10^{0}}$

$10^{-5} = \dfrac{1}{10^5}$ (par définition des exposants négatifs $a^{-n} = \dfrac{1}{a^n}$ pour tout $n \in \mathbb{Z}$ si $a \neq 0$)

$-10^5 = - 100~000 = \dfrac{- 100~000}{1} = \dfrac{- 100~000}{10^{0}}$$

$\dfrac{3.10^5}{10^7} = \dfrac{3}{10^2}$ par division des puissances ($\dfrac{a^m}{a^n} = a^{m-n}$ pour tout $m,n \in \Z$)

$\dfrac{10^7}{3.10^5} = \dfrac{10^2}{3} \simeq 33,333.... \notin \mathbb{D}$

Remarques

Les entiers relatifs sont des décimaux, car si $k \in \mathbb{Z}$, on peut aussi écrire $k=\dfrac{k}{1}=\dfrac{k}{10^0}$. On a donc la propriété $\mathbb{Z} \subset \mathbb{D}$.
Un nombre décimal possède une écriture décimale finie.

Nombres rationnels

Définition : Nombres rationnels

Un nombre rationnel est un nombre pouvant s'écrire sous la forme $\dfrac{a}{b}$ avec $a\in \mathbb{Z}$ et $b\in \mathbb{N}^{*}$ (c'est-à-dire $\mathbb{N}$ privé de $0$).

L'ensemble des nombres rationnels est noté $\mathbb{Q}$.

Remarque

Un nombre décimal est par définition un nombre rationnel.

Par définition de $\mathbb{D}$ et $\mathbb{Q}$, on a la propriété $\mathbb{D} \subset \mathbb{Q}$.

Propriété : Caractérisation des rationnels non décimaux

Tous les nombres rationnels ne possèdent pas d'écriture décimale finie. En particulier, $\dfrac{1}{3}$ n'est pas décimal.

Preuve

La démonstration de cette propriété sera faite plus tard dans l'année, dans le chapitre arithmétique.

Remarques

Les nombres rationnels non décimaux possèdent une écriture décimale infinie périodique, c'est-à-dire avec une série de chiffres qui se répètent à l'infini. Par exemple $\dfrac{1}{7} = 0,14285714285714...$ (on constate la répétition de la séquence 142857}).
Réciproquement, si un nombre possède une écriture décimale infinie périodique, alors c'est un rationnel.

Méthode : Déterminer une fraction égale à une écriture décimale infinie périodique

On considère le nombre $a$ dont l'écriture décimale est infinie périodique $a = 2,71347134...$. Démontrons que ce nombre est rationnel.

Solution

On constate que la partie répétitive des chiffres de $a$ est $7134$, donc de taille 4.

Donc $10^4 \times a = 10~000\times a = 27134,71347134...$.

D'où $10~000\times a - a = 27134,71347134... - 2,71347134... = 27134 -2 = 27~132$.

Or $10~000\times a - a = 9~999\times a$.

D'après les deux lignes précédentes, on a alors $9~999\times a = 27132$ soit $a = \dfrac{27~132}{9~999} = \dfrac{9~044}{3~333}$.

Donc $a$ est bien un nombre rationnel puisqu'il s'écrit sous la forme d'une fraction.

Application : Calculs avec les rationnels

ExerciceSolution

Dans chacun des cas suivants, calculer à la main chacune des expressions suivantes :

$A = \dfrac {5}{7} - \dfrac{3}{11}$

$B = -\dfrac {4}{3} + \dfrac{7}{8}$

$C = \dfrac {3}{8} - \dfrac{5}{12}$

$D = \dfrac {-6}{7} \times \dfrac{8}{9}$

$E = \dfrac {3}{2} \times \left(-\dfrac{7}{3}\right)$

$F = \dfrac {48}{35} \times \dfrac{25}{64}$

$G = \dfrac {4}{7} \div \dfrac{8}{21}$

$H = \dfrac{~~\dfrac{3}{4}~~}{\dfrac{18}{20}}$

$I = \dfrac{~~7~~}{\dfrac{5}{3}}$

$J = \dfrac{~~\dfrac{7}{5}~~}{3}$

$A = \dfrac {5}{7} - \dfrac{3}{11} = \dfrac {5\times 11}{7\times 11} - \dfrac{3\times 7}{11\times 7} = \dfrac {55}{77} - \dfrac{21}{77} = \dfrac{34}{77}$

$B = -\dfrac {4}{3} + \dfrac{7}{8} = -\dfrac {4 \times 8}{3 \times 8} + \dfrac{7 \times 3}{8 \times 3} = -\dfrac {32}{24} + \dfrac{21}{24} -\dfrac {11}{24}$

$C = \dfrac {3}{8} - \dfrac{5}{12} = \dfrac {3\times 3}{8\times 3} - \dfrac{5 \times 2}{12 \times 2} = \dfrac {9}{24} - \dfrac{10}{24} = - \dfrac{1}{24}$

$D = \dfrac {-6}{7} \times \dfrac{8}{9} = \dfrac{-6 \times 8}{7 \times 9} = \dfrac{-2 \times 3 \times 8}{7 \times 3 \times 3} = -\dfrac{16}{21}$ N'oubliez pas de simplifier !

$E = \dfrac {3}{2} \times \left(-\dfrac{7}{3}\right) = -\dfrac {3 \times 7}{2 \times3} = - \dfrac{7}{2}$

$F = \dfrac {48}{35} \times \dfrac{25}{64} = \dfrac{48 \times 25}{35 \times 64} = \dfrac{2 \times 3 \times 8 \times 5 \times 5}{5\times 7 \times 2 \times 4 \times 8} = \dfrac{15}{28}$

$G = \dfrac {4}{7} \div \dfrac{8}{21} = \dfrac {4}{7} \times \dfrac{21}{8} = \dfrac{4 \times 21}{7 \times 8} = \dfrac{ 4 \times 3 \times 7}{7 \times 2 \times 4} = \dfrac{3}{2}$

$H = \dfrac{~~\dfrac{3}{4}~~}{\dfrac{18}{20}} = \dfrac{3}{4}\div\dfrac{18}{20} = \dfrac{3}{4}\div\dfrac{20}{18} = \dfrac{3 \times 4 \times 5}{ 4 \times 3 \times 6} = \dfrac{5}{6}$.

$I = \dfrac{~~7~~}{\dfrac{5}{3}} = 7 \div \dfrac{5}{3} = 7 \times \dfrac{3}{5} = \dfrac{21}{5}$

$J = \dfrac{~~\dfrac{7}{5}~~}{3} = \dfrac{7}{5} \div 3 = \dfrac{7}{5} \times \dfrac{1}{3} = \dfrac{7}{15}$

Nombres réels

Définition : Nombres réels

Un {==nombre réel est un nombre exprimant une longueur, ou l'opposé d'un nombre exprimant une longueur.

L'ensemble des nombres rationnels est noté $\mathbb{R}$.

Remarques

Un nombre réel est un nombre dont le carré est positif ou nul .
Par définition, tous les nombres rationnels sont des réels. On a alors $\mathbb{Q} \subset \mathbb{R}$ .
Certains nombres réels ne sont pas rationnels. Par exemple $\pi$ n'est pas rationnel, tout comme $\sqrt{2}$ ( on le montrera en exercice ). Ces nombres sont dits irrationnels .

Propriété : Ensembles de nombres

Des remarques précédentes, on à la propriété :

\[ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{D} \subset \mathbb{Q} \subset \mathbb{R} \]

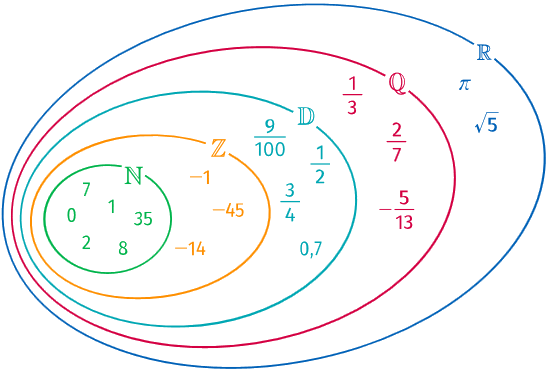
Diagramme de Veyn

Propriété : Droite des réels

Tout nombre réel est représenté par l'abscisse d'un point sur la droite numérique ( appelée aussi droite des réels ).

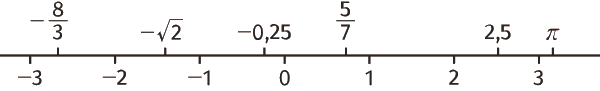
Application : Représenter sur la droite des réels

Déterminer l'abscisse de chacun des points de la droite ci-dessous :

Représenter la droite des réels ( unité : 5 ) et y placer le plus précisément possible les nombres suivants :

\[ 3 ~;~ -0,75 ~;~ \dfrac{5}{4} ~;~\dfrac{-2}{5} ~;~ \dfrac{7}{3} ~;~ \sqrt{2} \]